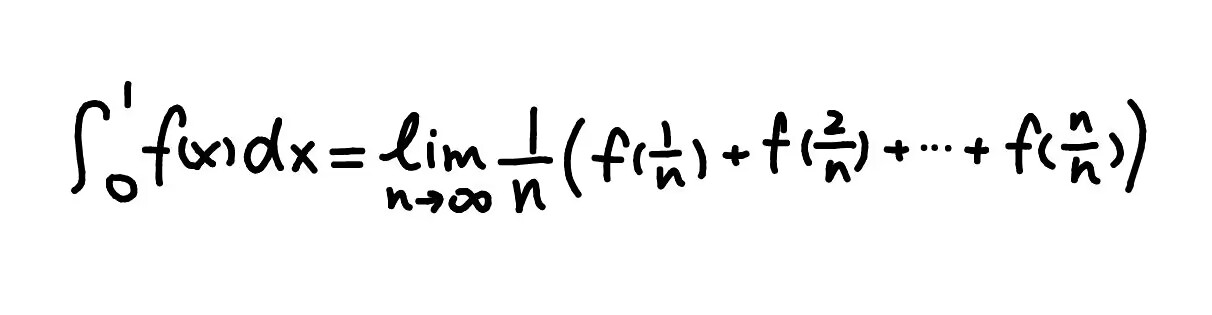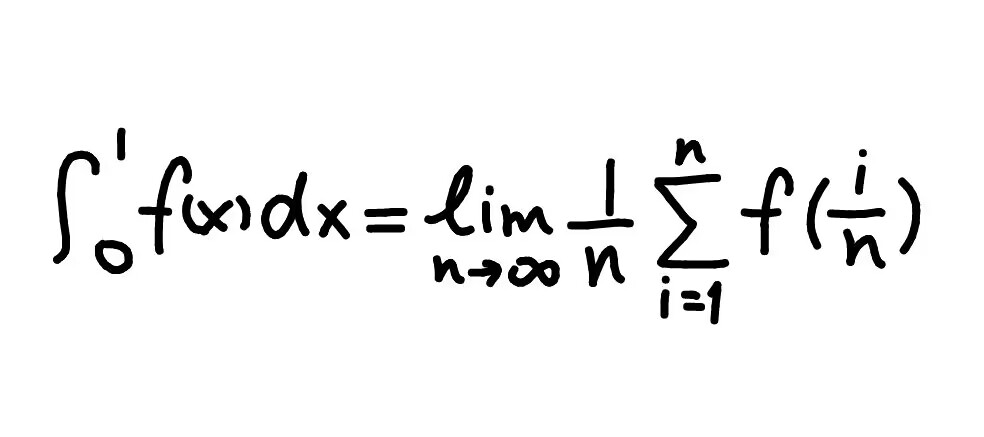∫cottdt=∫sintcostdt=
不定积分是求导的逆运算,求 f 的不定积分就是求哪个函数求导得到 f。
不定积分才有 C,
且同一个不定积分的 C 是相同的。
定积分 理解为 两数之差 时 使用 原函数作差。
定积分 理解为 面积 时 使用 被积分函数的图像 求面积。
分部积分法
∫uv′dx=uv−∫u′vdx
∫udv=uv−∫vdu
有理分式函数的不定积分
第一类换元法:∫g(F(X))f(x)dx=∫g(F(x))dF(x)
例:
===∫xsin(x2)dx121∫sin(x2)2xdx21∫sin(x2)d(x2)−21∫cos(x2)dx+C
第一类换元法也叫凑微分法,是说被积函数中的一部分可以与 dx 相乘变成 d别的东西 ,变完之后更好积,
例题里的 2x 恰好能与 dx 凑成 d(x2)
第二类换元法:∫f(x)dx=∫f(x(t))dtdxdt
例:∫exdx
令 t=x ,则 x=t2→dx=2tdt ,
回代得 原积分=∫et2tdt ,然后使用分部积分法。
反常积分
即瑕积分和无穷限积分。
瑕积分:积分区域包含瑕点的积分。
瑕点:函数值为 ∞ 的点。
无穷限积分:积分上下限为 ∞ 的积分。
语法糖
∫常数+∞=limh→+∞∫常数h
原函数的定义
如果 F′(x) 的导数是 f(x) ,则称 F(x) 是 f(x) 的一个原函数。
显然,如果 F(x) 是 f(x) 的一个原函数(即 F 导出 f ),则 F(x)+C 也会是 f(x) 的一个原函数( C 是常数)。
可以证明,f(x)的所有原函数只会是 F(x)+C 这一种形式
比如说 f(x)=2x 的一个原函数是 F(x)=x2 ,则 f(x) 的原函数只有 x2+c 这一系列,其他函数都不会是 f 的原函数。
这个定理我们不证。
不定积分的定义
2x 的全体原函数是 {x2+C∣C∈R} ,这是一个集合。
我们把这个集合简记为 x2+C ,称它为 2x 的不定积分。
所以其实不定积分是 Callable[函数,set[函数]] 。
积分常数 C 的性质
+C 是个语法糖
因为 全体常数+全体常数=全体常数,
所以 C+C=C,2C也=C。
不可积 函数
考虑 f(x) 是狄利克雷函数:
D(x)={1,0,x∈Q,x∈R\Q,
这个 f(x) 太怪了,没有函数能导出它来。
就是 f(x) 没有原函数,称 f(x) 不可积。
积不出 函数
现在考虑 f(x)=ex2 。
它有不定积分,就是有一个函数 F(x) 求导为 f(x),
F(x) 的图像可以画出来。
但是这个 F(x) 既不是 ex2,也不是 e(sinx)2,也不是 exx ……,
他既不是我们已有的函数(幂函数、指数函数、对数函数、三角函数等)的和,
也不是他们的有限次复合。
他就是一个普通的没名字的函数,我们无法通过别的语言描述他,
就是我们无法通过 2,ln,sin,arctan 等等这些符号描述它。
只能描述为 ex2 的不定积分。
比如 ex2 的不定积分是 (一个不能通过现有的符号表示的函数)+C 。
这种不定积分 存在,但不能被 ‘幂函数 指数函数 对数函数 三角/反三角函数 及其四则运算或有限次复合’ 表示。
我们说 ex2 的不定积分 存在但非初等,
称 ex2 积不出。
以下都是积不出的函数,不要尝试积分,不需要记忆。

0∼1 区间上定积分的定义
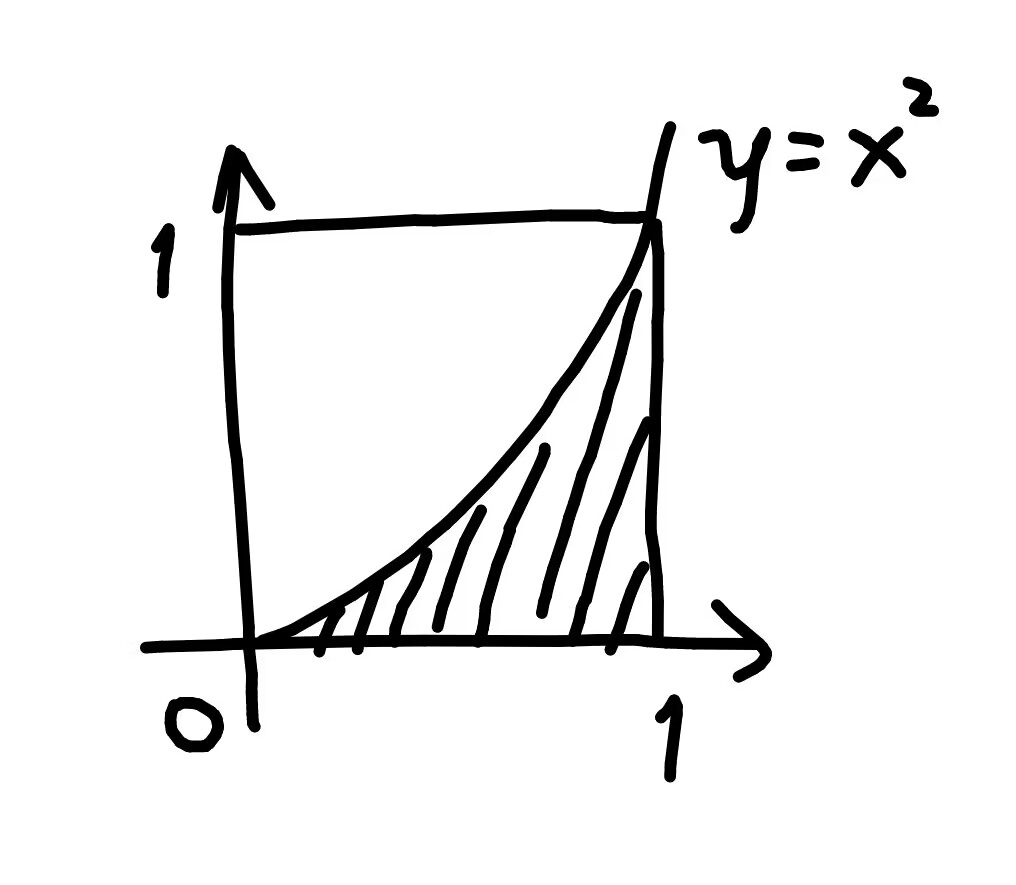
我现在要求阴影部分面积。
我取四个采样点:40,41,42,43。
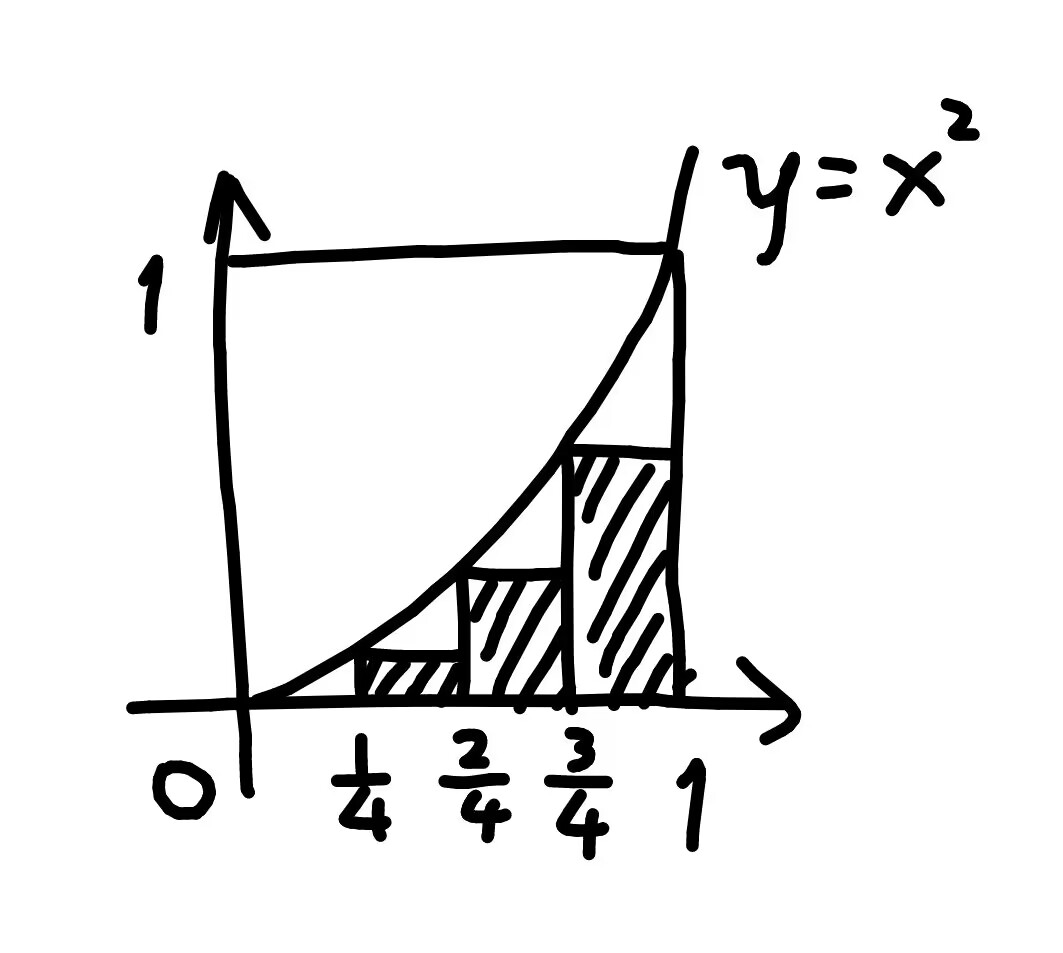
上图中阴影部分的面积是:
f(40)×41+f(41)×41+f(42)×41+f(43)×41 ,f(x)=x2 。
通过不断增加采样点数量,阴影部分面积会逐渐逼近所要求的大不规则图形的面积。
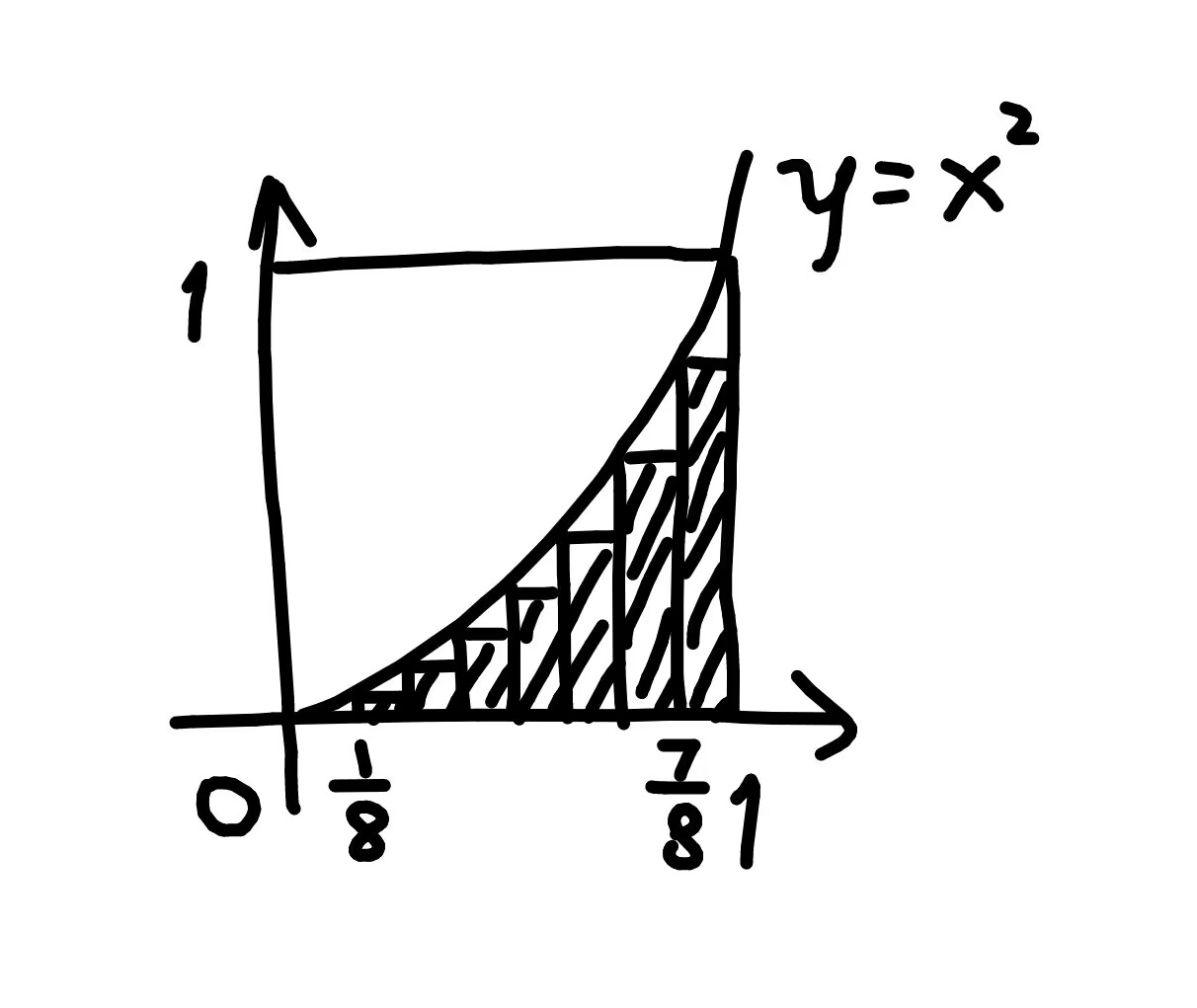
比如上图中的面积是 81×(f(80)+f(81)+f(82)+⋯+f(87)) 。
我取 n 个采样点,面积就是 n1×(f(n0)+f(n1)+f(n2)+⋯+f(nn−1)) 。
n→∞,这个极限式的结果就是所求不规则图形的面积。
12+22+⋯+n2=6n(n+1)(2n+1) 。
这是取了每一个矩形的左端点,
其实更常见的取法是取每一个矩形的右端点。
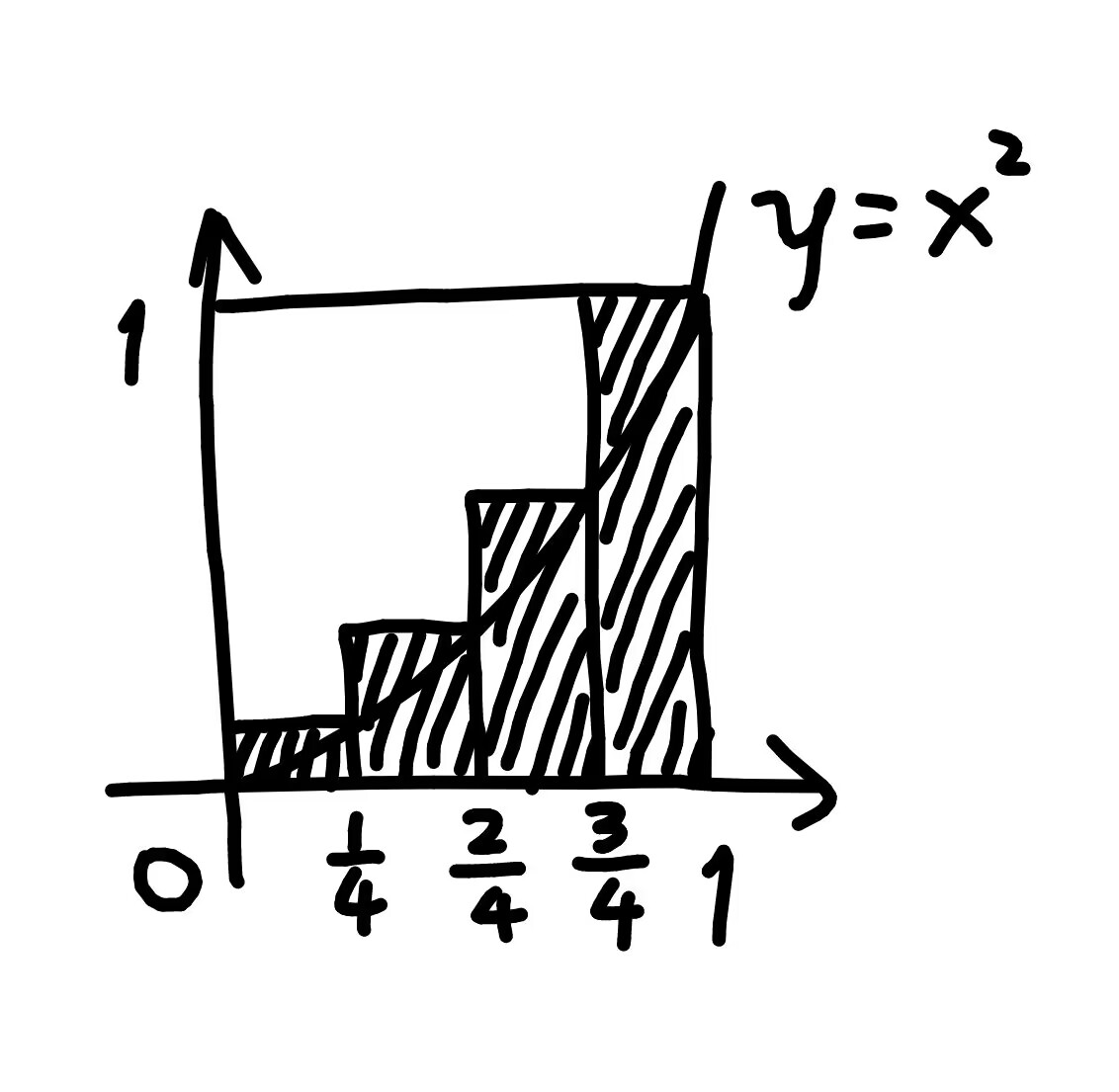
对应到这里是 41×(f(41)+f(42)+f(43)+f(44)) 。
n 个采样点是 n1×(f(n1)+f(n2)+⋯+f(nn)) 。
算出来的答案是一样的,但是更直接一点。
n 个采样点是 n1×(f(n1)+f(n2)+⋯+f(nn)) 。
把这个n→∞,就是函数 f 在 0∼1 区间的定积分
。
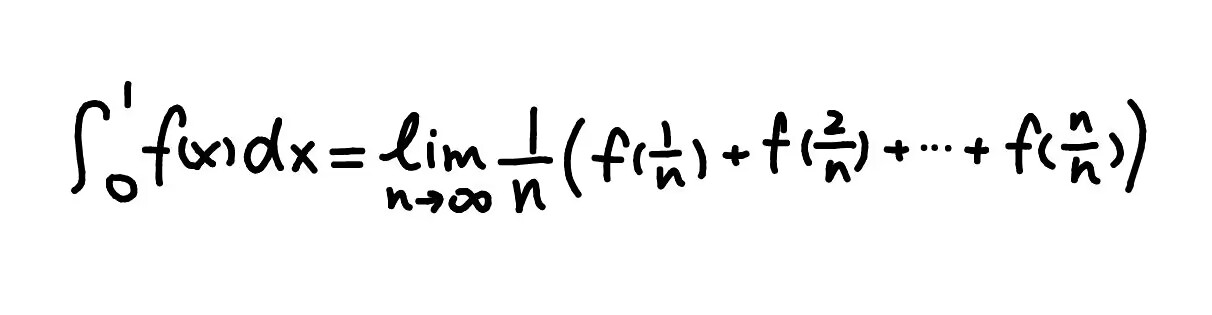
省略号太不优雅了,上大学要习惯使用求和符号 ∑ 。
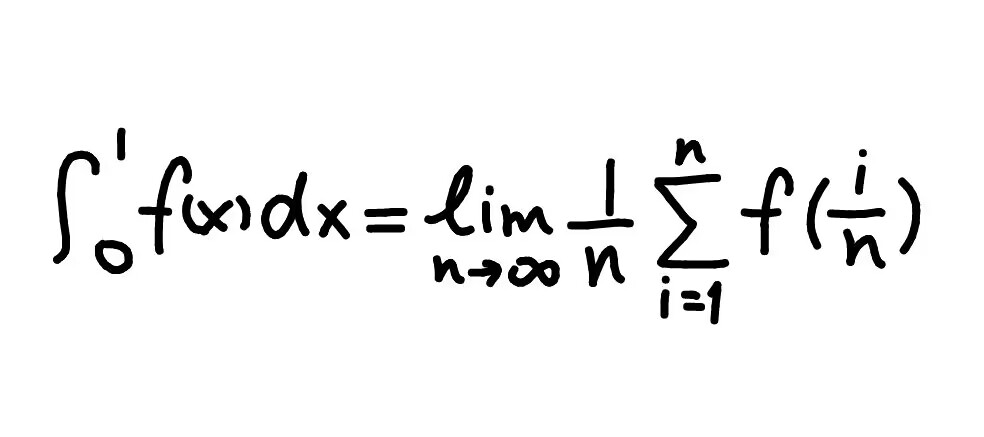
f(x) 在 0∼1 的定积分 = 要求的不规则图形的面积 = 刚才的极限式。
你可以回顾一下刚才的步骤,经历了 采样 → 求矩形的面积之和 → 求 n 到无穷极限 的步骤,分别对应着 f(ni),n1∑,和 lim 。